An essay on value
Scientific method and administrative decision
A submission to the NSW Minister for Planning and Environment on the Wingham Management Area Environmental Impact Statement, November 1992
The Tiger
The tiger paces up and down
Behind the black bars of the page,
His heart is smouldering with rage.
Captive within the lines of type
He seeks, and yet can never find,
The world where he was free to range:
He is the poet's furious mind.
His are the unblinking eyes that stare
Into the gold heart of the sun,
He rakes the sky of stars and hunts
The darkness down, and is not done.
His was the world to roam, who now
Is captive to the black-barred page.
Reader unlock the lines and face
The splendid danger of his rage!
Rosemary Dobson
This submission eventually became the occasion of a hearing in the NSW Land and Environment Court, JEFFREY NICHOLLS v DIRECTOR GENERAL NATIONAL PARKS AND WILDLIFE SERVICE No. 10151 of 1994. None of the issues raised in this submission were discussed in the Court. The Judgment is available on the web. Further discussion may be found in Brook et al which mentions this case.
Section I: The issue
Killing
1 We must kill to live. The question before is is whether or not to kill some fraction of the old growth forest (OGF) in the Wingham management area (WMA) in order to keep the sawmilling operation at Mt George alive.
Religion
2 Although the Environmental Impact Statement (EIS), as we have it, is a document based largely on resource, commercial and employment considerations, I believe the Commission is facing a religious issue, and will have no peace until it realizes that fact.
3 Matters of life and death are questions of religion. For those who have power over life and death, deciding what to kill is a question of value. The value system of any organism is determined by the history of its survival.
4 If the decision is good, the benefit from killing will exceed the value of what is destroyed, yielding a profit and enhanced probability of survival. A wrong judgment of value leads to the opposite result.
5 I assume that out of the infinity of actions which I can perform at any moment, what I am actually doing at this moment is calculated by my total system to be the optimal contribution to my survival in current circumstances. I think of my inner workings as a black box. I can see some of my input and some of my output. The conclusion that the output is optimized on the basis of the input seems to me to follow from my understanding of evolution.
6 This general notion holds for all organisms, from the simplest to the largest. An organism is a living system. We have mathematical tools to study the operation of systems. Our economic activity is an example of a living system, as is an old growth forest.
7 The economically driven debate about the value of the old growth forests brings us therefore, to a critical question: can systems theory tells us anything so general as to throw light on the problem of me and not-me myself and my environment?
8 This debate is being acted out concretely in the forests in the confrontation between the Forestry Commission of NSW and those blockading the forests. Between them stand the police. There is great public cost in this confrontation.
9 I went to the forest as a friend of a band and became involved in the action. I was privileged to observe the action from the top of a tripod. A video taken from this vantage point is enclosed with this submission, and is to be considered part of it.
10 As the Commission notes in its 1990-1991 Annual Report: The costs of continuing environmental challenges and the uncertainty they create should be recognized. Defending the Commission's operations in Court has cost $155 000 in 1990-91, and an increased provision has been made for 1991-92 . Added to this is the cost to the community of police action and lost production, and disruption to local economies. This points to the need for a mechanism to provide greater certainty for the Commission's management of the State's native forests.
Environmental law
11 I believe the issues at stake here are of the same social significance as that which faced the first Commissions to confront the problem of Aboriginal land rights. Like land rights, environmental rights are a religious issue.
12 Environmental rights are guaranteed by environmental law. We have only a few decades experience with environmental law. It is already becoming clear, however, that the piecemeal palliative approach taken to date is not powerful enough to deal with the enormity of the problems facing us.
13 A peaceful relationship between human beings and their environment is going to require a radical revision of our concepts about ourselves and the world. To get our environmental law right, we must get our understanding of our environment right.
14 Was the world created by a god who resides elsewhere; or is it itself divine? Has god given human beings sovereignty over the natural world; or are we part of the divinity itself, bound to live in harmony with the whole if we are to survive in peace?
15 I am a Christian who has come to realize that my religion, rather than being superior to that of Aboriginal people, is at best equal and possibly inferior to it. One should not be surprised at this. Aboriginal religion can claim a continuous history an order of magnitude greater than the Christian tradition.
16 It seems to me that we are witnessing a religious phenomenon in the forests. A small number of the descendants of christianity are trying to implement an Aboriginal view of land. I believe they are speaking for a much wider section of the population that see the destruction of the OGF as sacrilege.
17 To Christians, the land is a resource. To the Aboriginal it is a divine. In Christianity, god is made manifest in the person of Jesus Christ. In Aboriginal religion, as I understand it, god is made manifest in everything. I believe that there is no measurable contradiction between these two views when properly understood and implemented.
18 The religious nature of the issue is obvious in the behaviour of the people in the forests. As the video shows there is music and chanting. There is a strong belief that to destroy the OGF is to destroy something of our own flesh. Since human behaviour in the forests is as much part of nature as the hoppings of wallabies, I believe the EIS must take them into account.
19 Unlike wallabies, however, people can talk. From this I draw my recommendation: that you institute an open public inquiry into environmental rights on the scale of the Woodward Report and the Ranger Report.
20 This submission has two more sections. The first deals with the more general question of religion.
21 Section III applies the doctrine developed in section II to the present case.
22 I am trying to find grounds for judgment in an environmental issue. An inquiry is rather like a court. The advocates feed ideas to the judges who weigh them all and pronounce judgment. I am one such advocate.
23 Judgment requires a model, a picture of what happened. Advocates for each side compete in trying to establish or discredit a certain picture in the minds of the judges of what actually happened.
24 The first judgment I wish to argue for is that the world of experience is the manifestation of divinity. A model for this judgment is presented in section II. This judgment establishes a model in which to develop the judgment of section III: that the OGF be preserved in perpetuity as a wilderness.
Section II: Some theory
Administration
25 This submission is part of an administrative procedure designed to decide the fate of the OGF. As I see it, the existing EIS is not a sufficient foundation to make this decision. This is not the fault of its compilers, but of the administrative milieu in which brought it into existence.
26 I begin with the assumption that the task of administration is to keep the peace, and that this is to be achieved by providing, as far as possible, for the needs of everyone. Human need I take to be any any human input, such as food, living space or love, whose absence causes pain.
27 There are two complementary approaches to this task: one is to minimize need; the other is to maximize the availability of goods, that is things that satisfy human need.
28 The minimization of need, that is, the denial that certain needs exist and any consequent attempt to deprive people of the satisfaction of these needs, is not acceptable in a free society.
29 Religion is a good, the foundation of peace. I take religion to be the soul of a community, the common bond that binds people together to face collectively the difficulties of survival.
30 There has been and I believe continues a positive attempt in administrative circles to deprive the Aboriginal population of its religion. I also believe that the existing established religions have a strong positive tendency to deprive people of adequate religion because they maintain that ancient beliefs (such as the inferiority of women) should still be held in present times.
31 Since the Aborigines were deprived of their land and religion, we have seen the consequences of lack of religion: despair and dependence on drugs (particularly alcohol) to ease the pain. Many Christians have experienced similar pain when they have realized that their traditional religion can no longer cope with modern experience.
32 Historically, every tribe or language group had its own religion. Over the millennia, christianity has absorbed countless cultures, languages and religions into itself, justifying its activity by proclaiming itself the one true religion.
33 We are heirs to the enormous administrative experience gained in this process. The Romans were the administrators par excellence of the ancient world. They bequeathed their empire and administrative skills to the Roman Catholic Church, which in turn nurtured the Church of England and the British Empire which forced its administrative system on the people of Australia.
34 One of the strengths of this administration, like the English language, is that it is eclectic, prepared to incorporate words, ideas and procedures from anywhere into the system.
35 Here I propose that we extend our own administrative system by incorporating features of the Aboriginal system. Its incredible stability, if nothing else, must recommend it to us.
Scientific method
36 The foundations of administration are knowledge and power. One cannot work in the dark and hope for consistent success. Nor is there any use in knowing what to do without the power to make that knowledge effective in action.
37 Our most powerful route to knowledge is the scientific method, whose history can be traced to the misty beginnings of human literature. This EIS is an attempt to bring scientific knowledge to bear on an administrative problem.
38 The scientific method is a procedure for generating a reliable picture of our environment. The foundations of modern scientific method were formalized by Karl Popper in The logic of scientific discovery (Hutchinson, London 1959-80).
39 Science proceeds by constructing formal models of the world. A model is good if it accurately simulates the phenomena it is intended to model. A good model is not necessarily true, since other models may give an equally accurate simulation.
40 Although we cannot prove a scientific model true, we can prove it false by showing that it fails to give the correct outputs for certain inputs within its range. The mathematics of probability shows us that increasingly frequent application of a model without failure justifies greater confidence in it.
41 Scientific models give us great power by exposing the simple harmonies that lie beneath complex phenomena. The simple rules of arithmetic, for instance, provide us with deep insight into our economic system; computer models of forest and other crops allow us to predict future growth and yields.
Theology
42 Religion is a natural phenomenon. The science corresponding to religion is theology. Theology develops and tests models of god. In the present case we are seeking a theological model to harmonize Christian and Aboriginal religion.
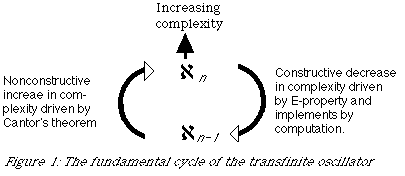
Mathematics
43 Mathematics is our richest and most general source of scientific models. Mathematics was once concerned principally with number, but developments over the last century or so have extended our mathematical vision to cover everything that can be expressed in symbols, that is everything that can be communicated.
A model of god
44 The foundation of mathematics is the theory of sets, founded by Georg Cantor. Cantor showed that the theory of sets is powerful enough to deal with infinite collections of symbols. The following discussion is meant for readers with some mathematical knowledge. You may avoid it if you wish and simply accept the conclusions presented in section III.
45 The smallest transfinite cardinal number ℵ0 is the least upper bound of the finite cardinal numbers 1, 2, 3 . . . . Using the theory of ordinal types, Cantor proved Cantor's Theorem (CT): given any transfinite set with cardinal number aleph(m), there exists a cardinal number aleph(m+1) and its associated ordinal number. CT establishes the ordered and unending formal hierarchy of cardinal and ordinal numbers called the Cantor Universe (CU). The CU, because of its unlimited size, is a natural choice to model god.
46 Traditionally, God is the creator and mover of the universe. In the model, creation and motion arise from consistency. The formal consistency of Cantor's proof demands that Cantor's theorem operate to make the transition between a system represented by aleph(m) and that represented by aleph(m+1). If we call this transition motion or creation, our model naturally explains these attributes of god. Let us call this formal source of motion Cantor Potential (CP) .
Pantheistic theory
47 A theory asserts that a given model corresponds to experience. The position I argue for here, pantheism , asserts that the universe is fittingly called god. This position is defensible if the model both meets the traditional specification of a model of god and can be shown to correspond to experience.
48 Christian mystical tradition tells us that the nature of god is so far beyond our ken that we cannot say what god is. We can only say what it is not. We assume that god is consistent.
49 Without going into further detail, I feel that the model is consistent with this tradition because it is a formal system whose structure arises purely from the non-constructive requirement of consistency. The model therefore specifies the boundaries of a consistent god. To go beyond the boundaries of the CU would be to step outside the realm of consistency.
50 So far we can point to three correspondences between the model and experience:
- Experience shows that formal systems (algorithms, texts or
protocols) can satisfactorily represent and communicate features
of the world. The CU is a formal system large enough to
contain all consistent formal systems. Since the whole of
mathematics may be derived from the theory of sets, the model is
rich enough to yield all the mathematical structures which have
been used to model the world.
- Experience comprises both discrete and continuous elements.
Cantor wanted to know the cardinal number of the continuum
(Hallett 1986, p 2). Although he felt that this number is the
second transfinite cardinal, ℵ1he could find no
proof. Subsequent work has shown that this continuum
hypothesis is independent of the axioms of modern set theory
(Cohen 1966).
Let us bypass this mathematical difficulty and introduce the terms relative continuity and resolvability. Say that a cardinal aleph(n) is continuous relative to aleph(m) if n > m, and that under this condition aleph(m) is resolvable by aleph(n). A set represented by aleph(n) is an unresolved continuum relative to aleph(m) < n. CT establishes a logical connection between discrete and continuous which suggests that they are both aspects of the whole. On this interpretation, the model accounts for the observed relationship between discrete and continuous.
- Every individual in the model is unique. The proof of CT is based on the relationship between cardinal and ordinal numbers. aleph(n+1) is the cardinal number of the aggregate of all ordinal numbers of cardinal number aleph(n). Each ordinal number is a distinct and unique mathematical object whose name is itself.
51 This observation has important consequences for the problem of universals (Landesman 1971). Part of the power of a scientific model is that one model can be applied to many different individuals or sets of circumstances. How can this be, if individuals are truly unique? The model answer is that unique individuals can have much in common. There are, for instance, aleph(n+1) ordinal numbers of cardinal number aleph(n). In a similar manner, distinct ordinal numbers may partially correspond to one another.
52 On the other hand, understanding does not require universality. We can, for instance, understand unique events, that is the execution of unique algorithms. Chaitin showed that an algorithm with all the redundancy removed is indistinguishable from a random number (Chaitin 1987).
53 Formal redundancy is the product of abstraction. By ignoring certain individual characteristics, we can treat a number of particles as though they were one, eg all members of the species homo sapiens.
A model proof for the existence of god
54 Let us start from the assumption that god is the mysterious creator of the universe of experience. Does god, so defined, exist? In the formal world exist means follows necessarily from the assumptions of the model.
55 A model represents some element of reality. If the representation is good, manipulations of the model (computations) reflect reality.
Computation
56 Soon after its discovery Cantor's universe soon began to throw up paradoxes that prompted a careful reexamination of the foundations of mathematics.
57 In 1928 Hilbert asked:
- Is mathematics consistent?
- Is mathematics complete?
- Is mathematics computable?
58 He expected three yeses but Gödel and Turing found that consistent formal systems of necessity generate both incomplete and incomputable elements.
59 Mathematics is complete if every mathematical statement that obeys the formal rules can be either proved or disproved. Mathematics is computable if there exists a definite mechanical process, like the execution of a computer program, which can decide whether a given proof works or not. The proof of completeness is thus logically dependent on the proof of computability.
60 Turing devised a universal machine that could execute all algorithms that can be represented as a one dimensional string of letters He then showed that there were processes that this Turing Machine could not complete.
61 Using the formalism of the machine, Turing transformed the problem of computability into a question about the relationship between ℵ0 the cardinal number of the set of natural numbers and ℵ1, the cardinal number of the set of reals, using the diagonal argument pioneered by Cantor. We can make this argument more general.
62 Algorithmic information theory defines the algorithmic information content I(x) of x as the size of the smallest program to calculate x (Chaitin op cit.). It then invokes Chaitin's Principle: if a theorem contains more information than a given set of axioms, then it is impossible for the theorem to be proved from the axioms.
63 In the case of the Turing Machine, this principle shows that a system whose complexity or information content is measured by ℵ1 cannot be computed by a system whose complexity is measured by ℵ0. We can extend this argument to get a transfinite hierarchy of computability : for n > m, a system whose complexity is measured by aleph(n) cannot be computed by a system whose complexity is measured by aleph(m).
64 Now assume that one system A may know another system B only insofar as B is computable using the resources of A. Assume further that insofar as the complexity of B is beyond the computing resources of A, we are justified in calling B mysterious relative to A (Greek, musterion = secret).
65 Since we know from Cantor's theorem that given any system X there must be a system of greater complexity Y, we are therefore guaranteed the existence of mystery for any system.
66 A similar argument shows that god controls the universe. Cybernetics is founded on principle of requisite variety (Ashby 1976): one system can only control another system if the controller is of equal or greater complexity than the controlled. Since the mysterious is mysterious because it is more complex than the knower, this principle also tells us that the the visible cannot control the mysterious. Since there is control (the system is stable) it must come from the mysterious.
67 The structure of the CU, therefore, points to the existence of a mysterious controller which we call god.
Me and not-me
68 One may object that the CU is too large to model the finite world, or, conversely, that the world is too small be be considered divine. But I am part of the universe, and so represented in the model by a certain cardinal number, aleph(i). Some things, therefore, are bounded from my point of view and others are not. In particular, I do not have the complexity to resolve my own upper bounds, but I can resolve my lower bounds. Some things are mysterious to me, others are not.
69 I am an individual component of the universe seeking to reflect its structure in myself and express my reflection in this text. So far I have modelled the universe using the CU, a static formal space existing in the world of mathematical symbols.
70 I now wish to extend the model to account for the process of knowledge or modelling as I experience it and apply the extended model to the universe as a whole.
The transfinite oscillator
71 I do this with a structure I call the Transfinite Oscillator (TO) which operates between different levels of the transfinite hierarchy. The increase in complexity is driven by CT. The decrease in complexity, corresponding to abstraction, knowledge or modelling is driven by a theorem of mathematical communication theory known as the McMillan's E theorem (Khinchin 1957 pp 54-58).
72 When we communicate, we do so using models of things, rather than the things themselves. The EIS, for instance, presents a particular model of the forest.
KNOWLEDGE
73 The force driving knowledge, the desire to know, arises from a potential inverse to the CP. Let us call this the E Potential (EP) because it corresponds to what is known as the E-property in the theory of communication.
74 In the light of the theory of evolution, we explain the natural desire to know by the competitive advantage that knowledge confers. An organism with knowledge of its environment is in a better position to predict future events and adjust its behaviour accordingly. The mathematical theory outlined here suggests that knowledge is not simply confined to living organisms, but is a fundamental component of all symbolic systems, and of the universe insofar as it is modelled by text.
75 The transfinite cardinal numbers aleph( ). are a natural measure of complexity. Their exponential structure makes a nice mathematical fit with the logarithmic scale usually chosen to measure entropy and complexity (Khinchin, op cit p 2).
76 A communication system is modelled as a source and a channel. Shannon founded information theory on a consideration of Markov sources. Khinchin extended the treatment to any ergodic source and any stationary channel with finite memory (Khinchin, op cit, p 30). Here I speculate on applying the theory to the CU. Space constrains me to speak only of sources.
77 Communication theory is an application of probability theory (Kolmogorov 1956).The output of a source is regarded as a random process. We take no heed of any 'meaning' which may be encoded in the output. The probabilistic structure of this process constitutes the mathematical definition of the given source.
78 The first part of the definition of source S is a set A of symbols called the alphabet of S whose elements are called letters. The second part of the definition of S is a measure of the probability of emission of sequences of letters, mu.
79 From this probability structure we can compute a number H called the source entropy which is a measure of the average amount of information carrying capacity per letter of the source output. The source is said to be stationary if the probability regime of its output does not change with time.
80 The only property of a source which concerns is here is the E-property established by McMillans's Theorem (Khinchin, op cit, pp 54-58). The E-property divides the set C of n letter words in the output of a given source into two groups known as the high probability group and the low probability group.
81 With the exception of the case when all the letters of the alphabet are equiprobable we find that for large n the high probability group contains only a negligibly small share of possible n letter words from the source. Almost all words fall into the low probability group. On the other hand, most of the entropy of a source is carried by words from the high probability group.
82 This fits our experience. Day to day English speech uses only a few thousand different words out of the hundreds of thousands we find in big dictionaries. Some little words used very frequently carry most of the traffic. The E-property is not confined to natural language, however, but applies to all ergodic sources.
83 Mathematics is a timeless formalism. A correct proof establishes relationships between symbols which are eternally valid. A source, on the other hand, emits a sequence of letters in time. By the time you have spoken the last sound in a sentence the first has died away. It no longer exists, and so cannot be talked about in the eternal present of mathematics.
84 It has become customary in physics and mathematics to represent time sequences by a mathematical space. In space-time graphs the time axis is drawn just like the space axis, and we treat all instants of time as existing simultaneously just like all the points in space. In general terms, a source is ergodic is we can satisfactorily study its behaviour in time through arguments in space.
85 Now without argument or proof, let us assume that the E-property allows us to encode almost all the information in a set of complexity aleph(n) using an alphabet whose entropy per letter is aleph(n-1) . This encoding I use as a model of knowledge..
86 It fits our experience of knowledge. Knowledge reduces complexity by abstracting the salient features of a situation. These salient features correspond in our model to the high probability sequences. Knowledge is an imperfect representation of reality. There is some information (corresponding to the low probability sequences) lost by confining our attention to the high probability sequences.
87 The number of different low probability sequences which lie outside the realm of knowledge is much greater than the number of high probability sequences, although individual low probability sequences are much rarer and more interesting. This corresponds to the common belief that the scope of the mystery in the universe is much greater than what can be known.
88 We are now in a position to draw a picture of the TO.
89 This extended version of the model enables us to see some more correspondences with experience. We can now model action, duality and measurement, matter and spirit, and life and death.
Action
90 Formalism in itself is dead, outside time. To test a formalism we must put it into action. Quantum mechanics has taught us that all observable processes in the universe are associated with a certain quantum of action measured in units of Planck's constant, h.
91 No action smaller than h is observed. This is seems consistent with mathematical theory, which requires well ordered sets for most of its proofs. A well ordered set is an ordered set with a smallest member. So we identify the observed quantum of action with the smallest element of the set of actions. Larger operations involve a countable discrete number of quanta, nh.
92 Let motion described by the TO be our model of action. This leads us to identify h with one cycle of the smallest oscillator, that whose smaller member in the smallest transfinite cardinal, ℵ0.
Duality and measurement
93 The idea of measurement implies a duality, the measure and what is measured. A measurement is a closed circuit. Measuring length, for instance, we record the readings on the tape at each end of the object to be measured, and subtract the smaller from the larger to get the length.
94 In the TO, knowledge is measured by creation and vice versa. This suggests, in accordance with experience, that every action has a creative element and a knowledge element, and that these elements have equal measure, that is they are of equal value.
Matter and spirit
94 Some belief on relationship between matter and spirit is an important element of religion. Here I will take them to be relative terms, defined in the first instance by the lower (material) and upper (spiritual) elements in the TO. Since the spiritual element is more complex, we can say on cybernetic grounds that spirit controls matter as outlined in the proof of god above.
96 Using the the model interpretation of matter and spirit, we say that knowledge of spirit yields matter, and the creative power of matter yields spirit. If we substitute land for matter, we interpret this to mean that the human spirit is born from the land and controls the land.
Life and death
97 Like the aleph(n) and the sets they represent, TOs can be nested inside one another. We notice in the universe that particles are nested. Looking inside myself, I am composed of cells, made of molecules, made of atoms etc. Looking outside, I find I am a small part of an ecosystem which is part of a planet which is part of a galaxy etc.
98 So let us use the TO to model individual organisms. Each organism is a stable system. The stability come from the more complex spiritual element of the organism. The existence of the spiritual element is sustained by the material element.
99 If either the spiritual or the material element fails, however, the organism ceases to exit. Death can come either form failure to control, or lack of something to control: one may starve for lack of food, or due to some personal disease.
Pain
100 In section I I proposed that the ultimate purpose of administration was the avoidance of pain. We are now in a position to model pain, and so define, in a negative way, the administrator's goal.
101 Pain resides in the spirit and arises when the material resources available to it are insufficient to sustain its own existence. Hunger is a simple example. The elimination of pain requires, then, manipulation of the material element of existence.
102 The power of spirit over matter increases as the distance between them increases. The model does not give absolute power to any spirit, because it is nested within a larger spirit. There are always circumstances outside the control of any spirit.
103 Although my spirit may not be able to manipulate my matter enough to eliminate my own pain, higher spirits, such as that of tribe, nation or planet may be able to do so. The larger the administrative unit devoted to the elimination of pain, the more chance it has of success. The minimization of human pain therefore demands global administration.
104 Obviously, if we had global law, police and social security, politically induced famine disasters that we witness almost continuously could be eliminated.
Physics
105 The final step in this modelling exercise is to expand the model to deal with the physical world. Although my spirit seems to be able to soar indefinitely, like the transfinite cardinals, my body is confined by physical constraints. If I do not conform to these physical constraints, pain and even death follow.
106 It is the need to increase the available living space that leads us to seek the optimum administrative response to physical constraints.
107 The foundation of physical constraint is symmetry and conservation. Physics studies natural motion. It seeks the invariant structures of the changing universe which we call principles and laws. Because these laws are invariant they can be written down and their formal representations remain true through time. The question before us is: can we harmonize the model of god presented here with the known laws of physics? I have not done much work on this problem, but believe there are possibilities.
108 So far I have presented a formal model of the universe based on symbolic computing. Einstein's special theory of relativity tells us first that the velocity of light c is the same for every observer, and second that things travelling at c are on the boundary of observable spacetime. Timeless formalisms therefore correspond in the physical world to things travelling at c. The realization of a formal model corresponds to the introduction of action, just as the realization of the rules of a game require actual play.
109 A Turing machine moves through a computation by a series of steps. Each step is a motion which changes the state of the computer. The steps are choreographed by the program, which may be a carefully constructed bit of software designed to achieve a certain result, or simply a set of random numbers. The details of the program do not matter here.
110 Each step is initiated by a clock pulse. We model a clock as a source with an alphabet of two letters emitted alternately. If we assume that the pulses are equiprobable, the entropy of a clock is 1 bit per letter.
111 We are using computation as a model of the universe. Let us assume that the clock of the universe is the simplest TO, TO(0), based on ℵ0 , the first transfinite number. We have already assumed that one cycle of TO(0) corresponds to one quantum of action, h .
Cantor Symmetry
112 In modern physics, the notion of conservation is closely linked to the notion of symmetry. Here wish to introduce symmetries which I call Cantor symmetry and ergodic symmetry, and one conservation law, conservation of action .
113 As I have presented it, the TO describes an oscillation between two levels of complexity represented by two transfinite cardinal numbers. The CU is a static structure. We model motion by the TO moving in the CU. The elementary motion in the CU lies between aleph(m) and aleph(m+1) . The complexity of this motion is measured by the subscript m. A TO modelling motion of complexity m may be written TO(m).
114 Because Cantor's proof is non-constructive, it simply allows us to distinguish between two possibilities, CT consistent, and CT inconsistent. The fundamental argument of the proof does not change with the complexity m of our position in the CU. All that changes is the input and output of the proof. We may say that CT is invariant with respect to complexity. As Cantor puts it To every transfinite number a there is a next greater proceeding out of it according to a unitary law . . . (my emphasis). (Cantor 1955 p 109).
115 As I understand it, the inverse of this unitary law is also a unitary law, and so we may say that the the model of knowledge represented by the TO is also invariant with respect to complexity. Insofar as human knowledge is modelled by the TO, it is no different from any other knowledge. From the point of view of the TO, the life and knowledge of a human being is indistinguishable from the life and knowledge of an electron.
116 We should therefore detect the same structures recurring at different levels of complexity. In particular, the Cantor cosmological principle underlies the analogy between the simple world of physics and the complex world of human politics and economy.
117 The conservation law corresponding to the Cantor symmetry is the conservation of action, nh.
Ergodic symmetry
118 The ergodic symmetry tells us that the information content of a system is invariant with respect to its encoding. I noted above that an ergodic source is one whose output in time can be represented by a structure in space.
119 There we were talking about physical space represented by a line, but the term space can be generalized to any structure. A language may be considered a space in this general sense, and it is common knowledge that the same ideas can be translated into different languages.
120 The two basic physical conservation laws arising from ergodic symmetry and conservation of energy and conservation of momentum, corresponding to two physical encodings of the same information. They arise through breaking of the Cantor symmetry. We may look at them as two different ways of expressing Cantor symmetry.
121 In a consistent world there can be no largest set, since CT tells us that any set generates a bigger one. Set theory does admit the existence of a smallest set, however, represented here in the transfinite realm by the smallest transfinite number, so that any aggregate of sets is bounded below.
122 The existence of a least member is a fundamental property of an ordered aggregate and underlies many mathematical proofs, since it gives us a starting point for establishing one to one correspondences. When we are talking about sets, we are talking about the abstract timeless space of mathematics.
123 When we come to talk about the TO, however, we are using the timeless formalism of mathematics to talk about action, which involves time. Let us imagine that there is an upper bound to time, but no lower bound.
124 We can make this idea plausible using the ergodic cosmological principle: since space modelled by the CU has a lower bound but no upper bound, we would expect time also to be bounded at one end and unbounded at the other.
125 Now the quantum of action appears to us as neither space nor time but as a mixture of both. In the model it is represented by the substitution of one symbol (element of space) for another which we call a logical operation (something that occurs in time). Such a logical operation is a step in a proof or a step in the execution of a computer program.
126 In computing, the size of a step is measured by the complexity of the symbols substituted. The substitution of the symbol 2 for the symbol 1+1 is a simpler step than the substitution of 22 for 11+11.
127 Practical computing also tells us that up to a point a fast computer taking little steps takes the same time to do a particular job as a slow computer taking big steps. There is a tradeoff between speed and word length.
128 We have ordered TOs in a spatial way, assigning the name TO(0) to the one with the smallest word length ℵ0 . Let us say that TO(0) operates at unbounded frequency, corresponding to the idea that the subdivision of time has no lower bound. Although we can assign no numerical value to such an unbounded frequency, let us nevertheless give it a symbol, f(n), so that we can assign processing power or bandwidth to TO(0) , B(TO(0)) =ℵ0 x f(n).
129 Let us make similar assumptions about a timewise ordering of TOs , naming the smallest member of this ordering to(0). Let us use aleph(n) to symbolize unbounded word length, and f(0)the minimum processing frequency. We can then write B(to(0)) = aleph(n) .f(0). The mathematical difficulties associated with evaluating these two expressions are reminiscent of Dirac's delta in quantum mechanics (Dirac 1983, p 58).
130 Suppose that we can attach some meaning to them, however, using the Cantor symmetry, and conclude that B(T(0)) = B(t(0)), that is that the bandwidth of our model universe is the same at both extremes of its development. This bandwidth is achieved at one extreme by unlimited word length and zero frequency (corresponding to the eternity of god) and at the other extreme by minimal word length and unlimited frequency (corresponding to the infinite power of god).
131 Again, relying on the Cantor symmetry, we can conclude that the bandwidth (processing power) of the universe is constant, ie B(T(m)) = B(T(n)) for all m and n. In other words, action is conserved with respect to complexity or word length , just as CT is invariant with respect to complexity.
The principle of least action
132 We need to establish one more correspondence between the model and modern physics before we can embark on a discussion of value. The principle of least action was first formulated by the French mathematician Maupertuis in 1744 (Yourgau 1979 p 19).
133 Whenever any action occurs in nature, he said (in French), the quantity of action employed in this change is the least possible. Euler established it as an exact dynamical theorem in the same year. The variational method, which seeks understand physical systems by finding the structure corresponding to the least action has proved very fruitful, and may be used to derive the major theories of physics.
134 Here, where we equate the quantum of action and the smallest observable operation of the universe, the principle of least action is equivalent to the search for the most efficient algorithm to perform a given action. In Darwinian terms, this most efficient program is the most likely to survive, since it achieves its task with the least resources.
135 The principle of least action or efficient algorithm gives us a means of selecting the observed world out of the immense space of possibility (entropy) represented by the CU.
136 The concept of efficient algorithm, formulated in the general space of the TO, can model an economy as easily as a subatomic particle, and so gives us means for expressing the concepts of economic efficiency and economic survival in a competitive system.
Value
137 Let us say the foundation of value is contribution to survival. The survival of an organism means its continuation through time. In order to get a grip on these ideas and establish their correspondences with the model, I wish to formulate the notion of survival in terms of communication.
138 Imagine that the past communicates with the future, and that an organism survives, ie endures from a point in the past t1 to a point in the future t2 by communicating its own structure from t1 to t2. This notion is obvious enough in the case of reproduction of living systems, since some at least of the communication from generation to generation is through a formal structure (message) expressed in genetic code.
139 Shannon's fundamental theorems of communication theory tell us that we can transmit a message virtually without error over a noisy channel provided we take our time and use the right coding system.
140 Without going into detail, we can assert that more complex coding algorithms (provided they are efficient) give more secure transmission than less complex ones. Since more complex coding algorithms are embodied in more complex organisms, we would expect more complex organisms to be more efficient at transmitting themselves into the future than simpler ones.
Security and complexity
141 Using communication theory, we can quantify the relationship between security and complexity, and so obtain an quantitative relationship between value and complexity.
142 The power to overcome noise in communication arises from redundancy. Given a channel with an alphabet Ai of n letters with probabilities pi (pi greater than or equal to 0, sum over i, pi = 1 ) we measure the information carrying capacity of the channel by the entropy H(A) = -sum over i, pi log pi(i = 1 . . . n) . If the probabilities pi are all equal this expression becomes H(A) = log n, and this can be shown to be the maximum possible entropy for an alphabet with n letters. We can then define a compression coefficient alpha for a given text and show that alpha = H(A) / log n . This compression coefficient is a measure of how much shorter the text could be made if the letters were used equiprobably (the most efficient use) rather than according to the given frequencies.
143 Now the essential problem in dealing with a noisy channel is to decide, from the symbol received, what symbol was sent. Thus if one is overhearing a conversation in a noisy room, the problem may be to decide, from what one heard, whether the speaker said six or sex.
144 From this example, it is clear that the problem is difficult if words sound almost the same. The more the transmitted and received symbols can be separated from one another, the less difficult the problem of distinction becomes.
145 We may think of each transmitted symbol as a point in a space. If many points are crowded into a small space, they are difficult to distinguish. If the space is made larger, the separation of the points becomes greater, and so eases the distinction problem.
146 The foundation of communication theory is that by encoding the message in blocks of letters, rather than single letters, the size of the space can be made to grow very much faster than the number of blocks, so that the space between the blocks grows much faster than the number of blocks. The blocks thus become more easily distinguishable, and the probability of error reduced.
147 Detailed consideration of the mathematics of the situation shows that the probability of error P is proportional to alpha -m where m is the size of the blocks of code.
148 If we now assume that the security S of transmission of the forest from one point in time to the next is the inverse of the probability of error, and equate the size of blocks of code m with the area A of the piece of forest in question, we arrive at the general conclusion that S is proportional to alpha raised to the power A, where alpha is greater than 1.
149 In other words, communication theory suggests that the probability of survival (and therefore, according to the assumption above, the value) of a piece of forest is an exponential function of its area. Its value as a timber resource, on the other hand, is a linear function of its area.
Section III: Environmental law
150 The modelling exercise of section II is more impressionistic than rigorous. It requires much more work beyond the time constraint on this submission and beyond my present understanding. I believe, however, that there is some truth in the above discussion which those charged with managing the forest can overlook only at their peril.
151 The model, since it is based on the general theory of text and communication, is big enough to express all communicable religious beliefs. My assumption in this section is that the mathematical constraints to be found in the model are also to be found in the world and in any belief system.
152 We are talking here about the extension of natural justice to the forests. Lord Reid, (Ridge v Baldwin [1963] 2 All ER 66 at 71]) suggests a preferred attitude to natural justice:
In modern times opinions have sometimes been expressed to the effect that natural justice is so vague as to be practically meaningless. But I would regard these as tainted by the perennial fallacy that because something cannot be cut and dried and nicely weighed or measured therefore it does not exist.
153 Assuming it proved that the world, including ourselves, is divine, it must follow that sovereignty over the world does not lie exclusively in human lawmaking apparatus. We must recognize the preexistence of laws which, according to the best of our scientific knowledge, are responsible for our own genesis.
154 With this extension of sovereignty must come an extension of natural justice. The implications of this position for environmental management are immense, but we once we establish beyond reasonable doubt that the argument for the position is valid, we must accept its consequences.
Value
155 My purpose, in this submission, has been to point out to you that the FCNSW (and therefore yourself) have a religious problem. There is a threat to the peace in the form of a struggle between Christian and Aboriginal views of this land.
156 By Christian, I mean the world view in which I grew, which entered the Australian continent in 1788. By Aboriginal, I mean that view that prevailed before the Christian view arrived.
157 The casualties to date have been of the order of one million Aboriginal people and most of Australia's natural heritage.
158 This looks like the makings of Christian victory. For a long time it has appeared that Christianity will succeed in cleansing the country of Aboriginal culture, and that the wilderness will all be shaped in the image of the Christian cosmopolis.
159 We are now beginning to see, however, that a Christian victory, like victory in the nuclear war that we have recently avoided, is tantamount to death. This war was, I believe, between two effectively Christian nations.
160 The universe is a wilderness beyond our taming. On the theory presented above, our institutions have very little survival value. They depend on a large quantity of material input: non-renewable energy and resources; and very little spiritual input: the complex and subtle codings that guarantee the survival of wilderness.
161 In the final analysis, I think the only true measure of the value of something is its contribution to our survival. Since the survival of any organism modelled by the TO depends on both matter and spirit, we must consider both in our consideration of value.
Freedom
162 I think the power to survive ultimately depends on freedom. I understand wilderness to mean as free as possible. There are laws in the wilderness, but they are laws with a divine tendency: they act to increase the distance between matter in spirit. In other words, they are in harmony with CT, which says (in terms of the various definitions above) that consistency demands the growth of spirit.
163 Christianity has brought us great freedom through its administrative power, but it has fettered the human spirit. The problem lies in the belief that wildness is dangerous. This belief relies in turn on the doctrine of original sin: that somewhere in the beginning something went wrong, and the world we have now (including our own nature) is flawed and need of outside control.
164 This outside control is provided by Christian law and Christian administration. We have seen the impact of this doctrine of original sin on a people whose religion is not founded on such a fault.
164 In the model developed above, the universe is divine and subject therefore to no outside constraint. God is wild.
Wilderness
166 As I noted in section II, the path from matter to spirit and the path from spirit to matter are of equal measure. These two paths are connected to form one cycle of action or operation.
167 The two paths are appropriately called creation and knowledge. We are capable of infinite creation. We have even created a device adequate to annihilate ourselves.
168 The TO is not a deterministic device. Of its nature, it includes mystery, and in mystery lies danger. We minimize danger by probing the mysteries, which include our own creations. We have created forestry: is it safe or dangerous? If it is dangerous, we can learn this either by looking, or by refusing to look and experiencing the inevitable crash.
Farming
169 The FCNSW is engaged in farming. Farming is our most necessary interaction with our environment, since it produces food, our personal material input. Farming is an example of knowledge, the path from spiritual to material.
170 Farms are places where we choose to kill the wilderness and nurture plants of our own choosing. We do this by depriving the wilderness of its material base and diverting this material to our own purposes.
171 Farming must be secure, for if it fails we die. How can we be secure? By keeping out of danger.
Always err on the safe side
172 The probability of falling over a cliff is some function of the distance between one's centre of gravity and the edge of the cliff. To feel secure, stay back a little from the brink.
173 We step back from the brink, because we can see it. Keeping out of danger means keeping a good lookout. Our collective guide to action is law. To live securely as a society, we must study our laws and their harmony with the laws of the environment, which are outside our control.
174 Investment in knowledge prevents disaster, and because knowledge is so cheap compared to disaster, the safety conscious administrator will always be inclined to look before leaping.
175 A thoroughgoing revision of environmental law is an enormous but necessary challenge. It is the sort of challenge that a clever country, one of the richest in the world, has a moral obligation to take up.
176 Nor is this a purely altruistic operation. Intellectual property has value, and its value is potentially infinite, since it is predominantly spiritual, and needs very little material underpinning, unlike, say, the mining industry.
177 With the advent of peace, the planet stands on the verge of immense economic development. There is nothing to suggest that every person on the world does not have the same right to live in comfort as the better off citizens of NSW. If, however, each person in the world were to consume as much of the world's natural resources and produce as much waste and pollution as each inhabitant of NSW, the planet would be doomed.
178 People will pay handsomely to avoid this doom. You, as a powerful Minister of one of the wealthiest political bodies in the world, are in a position to tap this wealth. An investment in security could well be a secure investment.
179 The first step, I believe, is a proper inquiry to set our our own house in order. Hence the recommendation of this submission.
The EIS
180 Foresters, one would hope, would be the last people to lose sight of the forest for the trees. I feel, however, that the authors of the EIS have done this, probably because they were working to a foregone conclusion. Section 7 appears to me to suggest some sort of bargain. The mill will remain open if the area of OGF available is reduced x% but not if it reduced x + y% (Table 7.1).
181 This bargain is founded on a rather nebulous suggestion that Alternative B might lead to closure of the mill:
A further 21% reduction in quota to Mt. George mill would result in a similar reduction in the value of production. Given the nature of the mill, the result of such a reduction in quota would be to make it a commercially unacceptable investment.
182 We are given no production, engineering or financial data to assess this statement; a severe omission that does not seem justifiable, even on the grounds of commercial confidentiality. One would certainly like to cross examine members of the Company on this matter, and see what undertakings the Company can make (bearing in mind its responsibility to shareholders) to keep the mill open if it is granted adequate material.
182 Sawmillers per se are not interested in forests, but in trees. The forest may produce the trees, but it is an impediment to sawmilling. The task of the Commission is to produce trees for sawmillers. This is established by legislation, and is the quid pro quo given by the State of NSW in return from taking the forests out of the direct control of the sawmillers.
184 The EIS is driven by the same legislative force that drives the Commission, the need to produce trees. The Commission, however, sees that it must produce trees in perpetuity. In this it represents a more spiritual approach than that necessary for sawmilling. The small amount of timber available from private lands suggests that sawmillers left to themselves would have cut the resource out long ago.
185 The Commission therefore conceives of forests as permanent producers of trees, that is, tree farms. The question then becomes: should the Commission farm all available forest, or should it leave some alone?
Subdivision of the world
186 I work here on the assumption that the the world is divine. From this I conclude that we must limit the scope of our activities on the planet, since we are just one form of existence among many.
187 We have the power to make the whole world over to ourselves, but we do not have the right. Our environment also has rights.
Environmental rights
188 What is the source of environmental rights? I give two answers: the nature of god and (as a consequence) human nature.
189 The nature of god is defined for us by the boundaries of divinity. We have a model based on the assumption that god is bounded by consistency. This model shows that the boundaries are continually growing, driven by consistency.
190 We are represented in this model as part of god. Our survival depends upon the same requirement of consistency. We must be consistent with our environment or die. If we are to preserve our own existence, therefore, we are bound by consistency to ascribe a similar right to life to our environment.
191 If we fail to recognize environmental right and simply rely upon our power, extinction will follow.
Performance
192 The existence of environmental rights must affect the operation of the Commission.
193 The Commission has published the following Mission Statement:
The Forestry Commission of New South Wales will ensure, by the application of scientifically based multiple purpose forest management, the conservation of all natural forest ecosystems in the State Forests and the sustainable development of adequate supplies of timber and other forest products, to the best advantage of the people of NSW (1990-91 Annual Report).
194 A basic right of the environment is to be free, that is to remain undisturbed. This requires that sections of the environment must be isolated, so far as possible, from human activity. This is accepted by our practice of setting aside environmental parks and reserves.
195 The question is: how much must be set aside? The correct answer is, I believe: as much as possible. Such a policy would be in harmony with the principle of least action: to provide for human needs with minimum resources.
196 By reducing our impact on the planet, we allow it to flower in other directions. Our need for materials drives down the complexity of the planet. We turn forests into trees.
Economics
197 Survival requires that the exercise of power must be constrained by right (expressed by law). The exercise of economic power falls within this stipulation.
198 The TO may be used to model economic activity. Money corresponds to the material pole of the economy, and goods to the spiritual pole. The goods in this case are trees and timber, the money wages and profits which eventually accrue to individuals.
199 Economic activity itself is the material pole of human existence. We all have a right to money and goods. Our right to money is is secured by our rights to employment and social security.
200 As the EIS stands, we must conclude that the preservation of the OGF will cost jobs. These jobs will be lost in the course of the Commission scientifically (ie with knowledge of natural law) carrying out its mission to the best advantage of the people of NSW.
201 The people who lose these jobs are entitled to be compensation from the people of NSW.
202 The implementation of environmental rights will require many people to change their employment. It is unlikely, however, that such a programme will reduce overall employment. At present we are living like children who do not clean up after themselves. When we begin to respect our environment and clean up, there will be more work, so more economic activity and more employment.
This submission eventually became the occasion of a hearing in the NSW Land and Environment Court, JEFFREY NICHOLLS v DIRECTOR GENERAL NATIONAL PARKS AND WILDLIFE SERVICE No. 10151 of 1994. None of the issues raised in this submission were discussed in the Court. The Judgment is available on the web. Further discussion may be found in Brook et al which mentions this case.
Some further reading
Books
| Cantor, Georg, Contributions to the Founding of the Theory of Transfinite Numbers (Translated, with Introduction and Notes by Philip E B Jourdain), Dover 1955 Jacket: 'One of the greatest mathematical classics of all time, this work established a new field of mathematics which was to be of incalculable importance in topology, number theory, analysis, theory of functions, etc, as well as the entire field of modern logic.' Amazon back |
| Chaitin, Gregory J, Information, Randomness & Incompleteness: Papers on Algorithmic Information Theory, World Scientific 1987 Jacket: 'Algorithmic information theory is a branch of computational complexity theory concerned with the size of computer programs rather than with their running time. . . . The theory combines features of probability theory, information theory, statistical mechanics and thermodynamics, and recursive function or computability theory. . . . [A] major application of algorithmic information theory has been the dramatic new light it throws on Gödel's famous incompleteness theorem and on the limitations of the axiomatic method. . . . ' Amazon back |
| Coston, A B, Nature Conservation in the Pacific, Australian National University Press 1973 Amazon back |
| Dirac, P A M, The Principles of Quantum Mechanics (4th ed), Oxford UP/Clarendon 1983 Jacket: '[this] is the standard work in the fundamental principles of quantum mechaincs, indispensible both to the advanced student and the mature research worker, who will always find it a fresh source of knowledge and stimulation.' (Nature) Amazon back |
| Ehrlich, Paul R, Population Resources Environment: Issues in Human Ecology, W H Freeman and Company 1970 Jacket: 'This book is the first comprehensive, detailed analysis of the worldwide crisis of overpopulation and the resulting demands on food, resources and the environment. Taking a broad ecological approach, the Ehrlichs demonstrate that problems of modern society . . . are closely interconnected and that together they constitute a challenge without precedent in human history.' Amazon back |
| Frith, H J, Wildlife Conservation, Angus and Robertson 1973 Amazon back |
| Hallett, Michael, Cantorian set theory and limitation of size, Oxford UP 1984 Jacket: 'This book will be of use to a wide audience, from beginning students of set theory (who can gain from it a sense of how the subject reached its present form), to mathematical set theorists (who will find an expert guide to the early literature), and for anyone concerned with the philosophy of mathematics (who will be interested by the extensive and perceptive discussion of the set concept).' Daniel Isaacson. Amazon back |
| Kolmogorov, A N , Foundations of the Theory of Probability, Chelsea 1956 back |
| Landesman, Charles, The Problem of Universals, Basic Books 1971 back |
| Popper, Karl Raimund, The Logic of Scientific Discovery, 1992 Jacket: 'A striking picture of the logical character of scientific discovery is presented here . . . Science is presented as . . . the attempt to find a coherent theory of the world composed of bold conjectures and disciplines by penetrating criticism.' Amazon back |
